2023.09.14 - [기타] - Average Filter, 평균 필터
Average Filter, 평균 필터
평균 (Average) - 모든 데이터의 합을 데이터의 개수로 나눠준 값. 평균 필터 (Average Filter) - 실시간 데이터들의 평균을 구하고, 새로운 데이터를 포함하여 새로운 평균을 구하는 방법. 평균 필터 수
wjs7347.tistory.com
2023.09.15 - [기타] - Moving Average Filter, 이동 평균 필터
Moving Average Filter, 이동 평균 필터
2023.09.14 - [기타] - Average Filter, 평균 필터 Average Filter, 평균 필터 평균 (Average) - 모든 데이터의 합을 데이터의 개수로 나눠준 값. 평균 필터 (Average Filter) - 실시간 데이터들의 평균을 구하고, 새로
wjs7347.tistory.com
Moving Average Filter의 단점
- Moving average filter는 현재 데이터를 기준으로 뒤로 N개만큼의 평균을 이용해서 노이즈를 제거하는 방식이다.
- 하지만 이는 과거 N개의 데이터와 현재 새로 추가되는 데이터가 동일한 중요도를 가지고 계산된다는 단점이 존재.
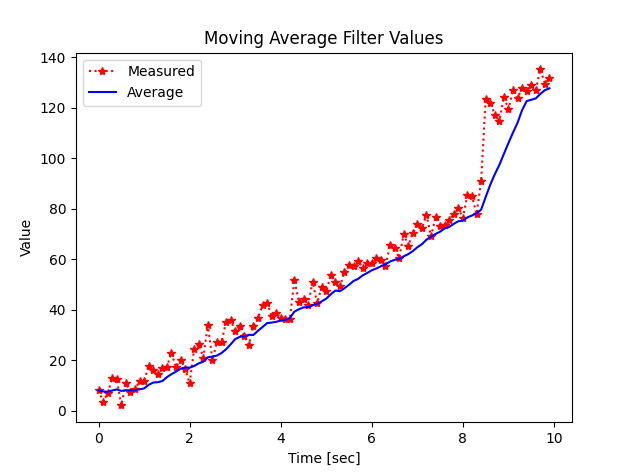
- 8초 구간에서 급격히 변화하는 측정값과 뒤 N개의 측정값을 동일한 비율로 1/N 하기 때문에 측정값을 부드럽게 따라가지 못한다.
Low-Pass Filter (LPF)
- 저주파 필터(LPF)는 이러한 이동 평균 필터의 단점을 보안하는 방법이다.
- 과거의 측정값보다 현재의 측정값에 더 많은 가중치를 두고 계산하는 방식이다.
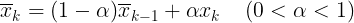
- x^_k-1 : 이전 추정값
- x_k : 현재 측정값
- 위 식처럼 현재 측정값에 alpha 만큼의 가중치를 더 두어 평균을 구한다.
LPF Python 코드
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
def get_meas(i):
"""Measure value"""
n = np.random.normal(0, 4) # n : 측정 노이즈
mean = i # 평균 측정
meas = mean + n # 측정 값
return meas
def low_pass_filter(x_meas, x_esti):
"""Calculate average sonar using a low-pass filter."""
x_esti = alpha * x_esti + (1 - alpha) * x_meas
return x_esti
time_end = 10
dt = 0.1
time = np.arange(0, time_end, dt)
n_samples = len(time)
x_meas_save = np.zeros(n_samples)
x_esti_save = np.zeros(n_samples)
alpha = 0.7 # 알파값 지정
x_esti = None
for i in range(n_samples):
k = i + 1
if k > (n_samples - 15):
k += 30
x_meas = get_meas(k)
if k == 1:
x_esti = x_meas
else:
x_esti = low_pass_filter(x_meas, x_esti)
x_meas_save[i] = x_meas
x_esti_save[i] = x_esti
plt.plot(time, x_meas_save, 'r:*', label='Measured')
plt.plot(time, x_esti_save, 'b-', label='Low-Pass Filter')
plt.legend(loc='upper left')
plt.title('LPF Values')
plt.xlabel('Time [sec]')
plt.ylabel('Value')
plt.savefig('png/low_pass_filter.png')
- low_pass_filter() 함수에서 LPF 수식을 계산하여 필터값을 계산.
- alpha값은 임의로 0.7.
- 현재 측정값 변화에 필터값이 잘 따라가는지 확인하기 위해 k가 n_sample - 15보다 클 경우 +30.
결과

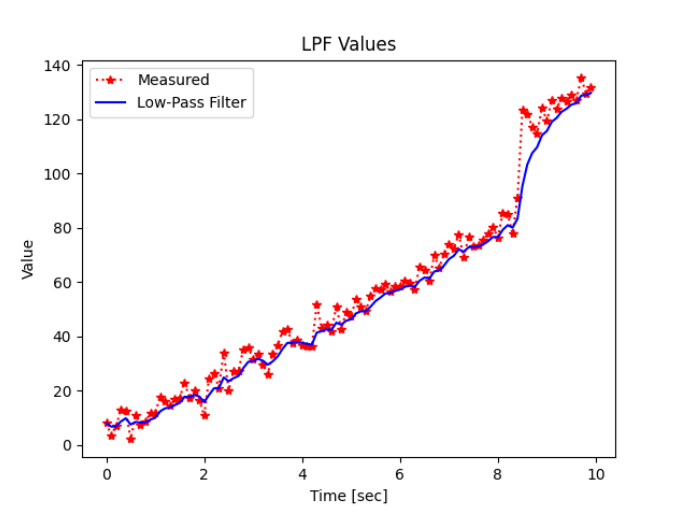
- 이동 평균 필터와 비교하여 현재의 측정값에 가중치를 두어 필터값을 구하기 때문에 변화에 잘 따라가는 모습.
'기타' 카테고리의 다른 글
| [GitLab] GitLab Visual Studio 2022 연동 (1) | 2023.11.24 |
|---|---|
| Kalman Filter, 칼만 필터 (0) | 2023.10.12 |
| Moving Average Filter, 이동 평균 필터 (0) | 2023.09.15 |
| Average Filter, 평균 필터 (0) | 2023.09.14 |
| detectron2 install error (0) | 2023.07.07 |