2023.09.15 - [기타] - Low Pass Filter, 저주파 필터
Low Pass Filter, 저주파 필터
2023.09.14 - [기타] - Average Filter, 평균 필터 Average Filter, 평균 필터 평균 (Average) - 모든 데이터의 합을 데이터의 개수로 나눠준 값. 평균 필터 (Average Filter) - 실시간 데이터들의 평균을 구하고, 새로
wjs7347.tistory.com
저주파 필터의 한계

- x^_k-1 : k-1까지의 평균
- x_k : 현재 측정값
- 저주파 필터는 현재 측정값에 alpha만큼의 가중치를 두어 현재 값을 계산해 주는 방식이다.
- 하지만 이 방식은 가중치를 미리 결정하여 변경시키지 못하기 때문에 한계가 있다.
칼만 필터
- 칼만 필터는 이러한 가중치(칼만 이득)가 필터가 수행되면서 알고리즘에 의해 지속적으로 변화하는 필터이다.
- 칼만 필터는 측정값을 입력으로 받아, 알고리즘에 의해 추정값을 출력한다.
- 출력한 추정값을 다음 단계에서 다시 사용하는 재귀적 알고리즘이다.
칼만 필터 알고리즘
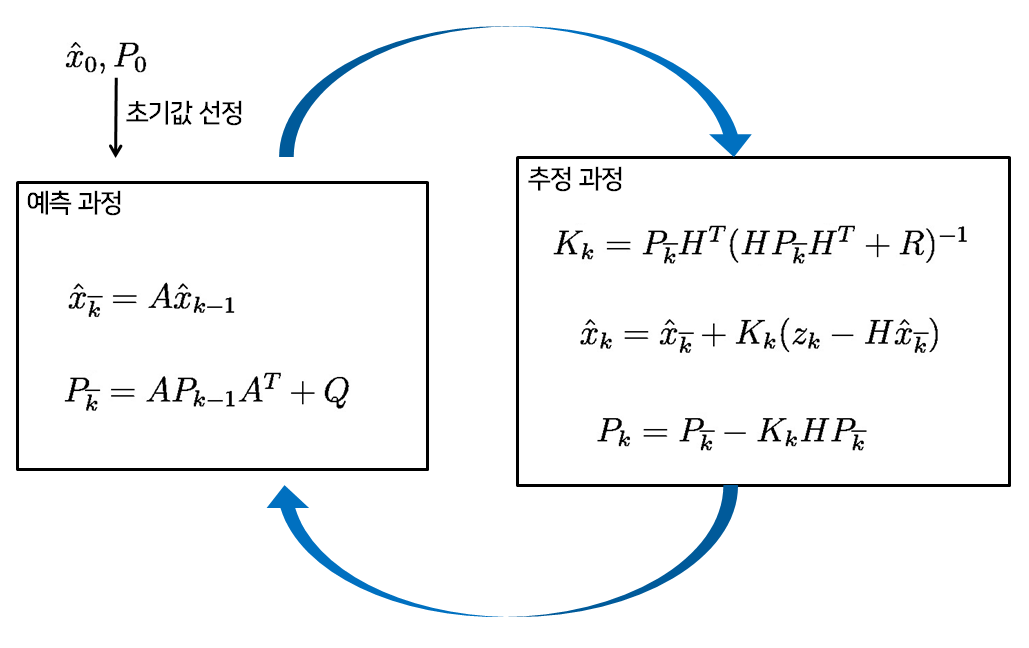
- 칼만 필터는 예측, 추정 과정으로 나뉜다.
- 추정 과정의 결과인 추정값(x)과 오차 공분산(P)이 다시 예측 과정에서 쓰이는 재귀적 알고리즘.
예측 과정

- 예측 과정에서는 이전 단계의 추정값을 사용하여 새로운 추정값을 예측한다. (-> 예측값 계산)

- 예측값 : (이전 상태 추정값 x A) 계산을 통해 현재 추정값을 예측하는 값.
- 오차 공분산 예측값 : 예측값이 평균을 기준으로 어느 정도 분포되어 있는지 나타내는 예측값의 오차 공분산.
- A : 이전 추정값을 통해 현재 추정값을 예측할 때 사용되는 행렬. (예시:현재위치=과거위치+움직인 시간*과거속도)
- Q : 시스템 노이즈
추정 과정

- 추정 과정에서는 칼만 이득(가중치)을 계산하고 예측값과 측정값을 토대로 추정값을 계산.

- 칼만 이득 : 오차 공분산 예측값과 측정값 노이즈에 의해 계산되는 가중치이다.
- 추정값 : 예측값과 칼만이득, 측정값에 의해 추정되는 출력값.
◎ 칼만 이득에 대한 부가 설명

추정값(x) 계산에 있어...
- 측정값 노이즈(R)가 작아지면 칼만 이득(K)이 커지게 되어 z-x'(측정값과 예측값의 차이)가 많은 영향을 미치게 된다.
- 반대로 오차공분산의 예측값(P')이 작아지게 되면 칼만 이득(K)이 작아지게 되어 z-x'의 영향이 작아지게 된다.
'기타' 카테고리의 다른 글
| Library, API, SDK, Framework (4) | 2024.01.04 |
|---|---|
| [GitLab] GitLab Visual Studio 2022 연동 (1) | 2023.11.24 |
| Low Pass Filter, 저주파 필터 (0) | 2023.09.15 |
| Moving Average Filter, 이동 평균 필터 (0) | 2023.09.15 |
| Average Filter, 평균 필터 (0) | 2023.09.14 |